Generating amazing mosaic photos from a bunch of boring photos
Posted on Thu 05 June 2014 in fun
How many times did it happen to you that you went on a trip where you took a lot of photos, got back home, browsed through the album and thought: "Oh, how I wish I could combine all of these photos and put them into a rectangular grid which will, when I view it from afar, look like this picture of Big Ben that I took and that I'm really proud of!"?
I can't hear what you answered, so I can just assume you answered "EVERY TIME!" and continue with this brand new blog post about generating mosaic photos using the power of python, openCV and integral images.
I didn't understand a word you're saying!
What we want to do is, given an album of photos and the photo shown on the left, generate the mosaic photo shown on the right. Yaaaaay!


Why would you want to do that? The quality of the result is crap!
Hey, we don't use this kind of language here! The quality is poor, not crap! BUT! If you zoom into the picture on the right, you will see that it's made of tiny little itty bitty photos! Hoooorraay!
Look!

If we zoom in closer to the moon, we'll see that the sky actually consists of pictures of a plane window. The moon is made of some pictures taken from the plane, a picture of something that I don't remember what it is AND, the best part, a photo of the statue of Peter Pan in Hyde Park! Yay!
Cool. How do we do it?
It's so simple it's stupid. Just take the photo we want to turn into a mosaic, loop through all the small patches that we want to replace with photos, calculate the average color of each patch and replace it with the photo which has the closest average color. That's it, wooohoo!
How to calculate the average color of a patch?
The obvious way of doing it is just to iterate through all of the pixels in the patch, summing the R, G, B values of the color and then dividing them by the number of pixels. Yes, it works, but if the patch is of size $N \times M$, with $N$ and $M$ being reaaaally big numbers, it will be slow. Some people would say that the time complexity of that would be $O(N \times M)$.
We can do it faster, we have the technology!
There are these things called Integral images or, as some call them, Summed area tables. A short example is shown below, but a better explanation can be found at the link above.
The integral image would be a matrix in which each element is the sum of elements left and above of it in the original image (and the element itself).
Anyway, for an toy example image looking like this:
\begin{equation} X= \begin{bmatrix} 9 & 5 & 2 & 1 & 2 \ 9 & 6 & 0 & 7 & 4 \ 8 & 9 & 1 & 3 & 3 \ 0 & 6 & 9 & 4 & 5 \ 3 & 2 & 6 & 9 & 3 \ \end{bmatrix} \end{equation}
The integral image would be:
\begin{equation}
I(X)=\begin{bmatrix}
0& 0& 0& 0& 0& 0 \
0& 9& 14& 16& 17& 19 \
0& 18& 29& 31& 39& 45 \
0& 26& 46& 49& 60& 69 \
0& 26& 52& 64& 79& 93 \
0& 29& 57& 75& 99& 116
\end{bmatrix}
\end{equation}
Why are they useful? Because you can calculate the sum of all of the elements in any submatrix (or patch in image) in constant time, that is in $O(1)$. Wow, so fast!
So, the sum of the elements in the rectangle with top left corner at $(1, 1)$ and bottom right corner at $(2, 3)$ of the original image would be calculated by $sum = I(3, 4) - I(1, 4) - I(3, 1) + I(1, 1)$, where $I$ is the integral image.
If we plug in the numbers, we'll get $sum = 60 - 17 - 26 + 9 = 26$, which is the same thing we would get if we summed $6 + 0 + 7 + 9 + 1 + 3 = 26$! I know, right? It's magic!
Does it work?
Let's see! Now that we know how to get the average color of a patch,
let's loop through our image and replace every patch with its average
color! If we had 25 patches vertically and 25 patches horizontally, our
new image would look like this shown on the left side and if we chose to
have 75 patches vertically and 50 patches horizontally, we would get the
picture shown on the right side:


They both look like low resolution pictures which means it works! Yay!
Let's do the real stuff!
The only thing we need now is to use real images instead of just the average color. First we need to get our album and calculate the average color of every photo in it. This can also be done using integral images; the bottom right corner value of the integral image will be the sum of all elements in the original image. Color images have three channels (red, green and blue; or blue, green and red as by default in OpenCV), so integral images of color images will also have three channels. Anyway, dividing the bottom right corner value with the image size gives us the average color of the whole image.
And now?
We are looping through the image, we found the patch average color and then what? We have to find which image in our album has the color that is the closest to the current one. We can do this by calculating the Euclidean distance of each color in our set to the current one and taking the one with the lowest distance. That's it! After that we just scale the image to fit our patch, put it there and move on!
Give me the code!
Here's the code! I was lazy so the path to the photos folder, the path to the image we want to turn into a mosaic and the number of patches are hardcoded. That's not good practice, don't do that! :D
import cv2
import os
import numpy as np
import math
#############################################
# configurable part here: #
#############################################
all_images_path = 'images/'
extension = '.jpg'
image_to_process_path = 'eiffel.jpg'
num_horizontal_images = 75
num_vertical_images = 100
#############################################
class Color:
def __init__(self, r, g, b):
self.r = r
self.g = g
self.b = b
def distance(color_1, color_2):
#just return the 3d euclidean distance
return math.sqrt((color_1.r - color_2.r) ** 2 +
(color_1.g - color_2.g) ** 2 +
(color_1.b - color_2.b) ** 2)
def get_avg_color_in_area(image, tl_x, tl_y, br_x, br_y):
#if this is an integral image
##############
# A-----B #
# | | #
# D-----C #
##############
#then the area of the ABCD rectangle can be computed
#as easy as c - b - d + a
a = image[tl_y, tl_x]
b = image[tl_y, br_x + 1]
c = image[br_y + 1, br_x + 1]
d = image[br_y + 1, tl_x]
#sum of all values in the b, g and r channels
sum_bgr = c - b - d + a
#this is the current area height times the current area width
area = (br_y + 1 - tl_y) * (br_x + 1 - tl_x)
#and here we get the average values for each channel
avg_bgr = sum_bgr / area
return Color(avg_bgr[2], avg_bgr[1], avg_bgr[0])
#opencv windows
cv2.namedWindow('image_to_process', flags = cv2.cv.CV_WINDOW_NORMAL)
#all the images from given path
image_paths = sorted([os.path.join(all_images_path, s)
for s in os.listdir(all_images_path)
if s.endswith(extension)])
#here we'll store the average color of an image at given path
color_path_list = []
curr = 0
#calculate the average color for each image in our image set
for image_path in image_paths:
#read current image
current_image = cv2.imread(image_path)
print current_image.dtype
#calculate the integral image
current_integral_image = cv2.integral(current_image)
print current_integral_image.dtype
#get the average color for the whole image
avg_color = get_avg_color_in_area(current_integral_image, 0, 0,
current_image.shape[1] - 1,
current_image.shape[0] - 1)
#let's save this info somewhere
color_path_list.append((avg_color, image_path))
#and just print how many images we processed
curr += 1
print curr, '/', len(image_paths)
#aaaand let's process the image we want to process
image_to_process = cv2.imread(image_to_process_path)
#look, it's here
cv2.imshow('image_to_process', image_to_process)
#calculate its integral image because integral images are cool
image_to_process_integral = cv2.integral(image_to_process)
#get the dimensions of small images
image_h = image_to_process.shape[0] / num_vertical_images
image_w = image_to_process.shape[1] / num_horizontal_images
#here we'll store the distances of all the colors we have from
#the color we need. and then we just use the nearest available
distances = np.zeros(len(color_path_list))
#just to make things a bit faster, we'll store the already
#resized small images into this dictionary as we use them
#so that we don't have to load each image again and again.
cached = {}
for r in xrange(num_vertical_images):
for c in xrange(num_horizontal_images):
#the average color of the current image patch
avg_color = get_avg_color_in_area(image_to_process_integral,
c * image_w, r * image_h,
(c + 1) * image_w - 1,
(r + 1) * image_h - 1)
#let's calculate the distance of each color in our set
#from the current average color
for i in xrange(len(color_path_list)):
distances[i] = distance(avg_color, color_path_list[i][0])
#the index of the closest color
index = (np.abs(distances)).argmin()
#and the path of the image which has this average color
nearest_image_path = color_path_list[index][1]
#if we haven't already used this image, then load it and resize it
if (not nearest_image_path in cached):
nearest_image = cv2.imread(nearest_image_path)
resized = cv2.resize(nearest_image, (image_w, image_h))
cached[nearest_image_path] = resized
else:
#otherwise just use the cached one
resized = cached[nearest_image_path]
#replace the pixels in the original image with the small image with
#the correct average color
image_to_process[r * image_h : (r + 1) * image_h,
c * image_w : (c + 1) * image_w] = resized[:, :]
#display the current progress of our mosaic
cv2.imshow('image_to_process', image_to_process)
#wait a bit
cv2.waitKey(10)
#save the generated image
cv2.imwrite('mosaic.png', image_to_process)
#wait for the user to press a key
cv2.waitKey(0)
The code is also available on github.
Give me a gif!
OK! Click here.
Give me a better gif!
OK! Click here
I don't like the Big Ben!
OK.
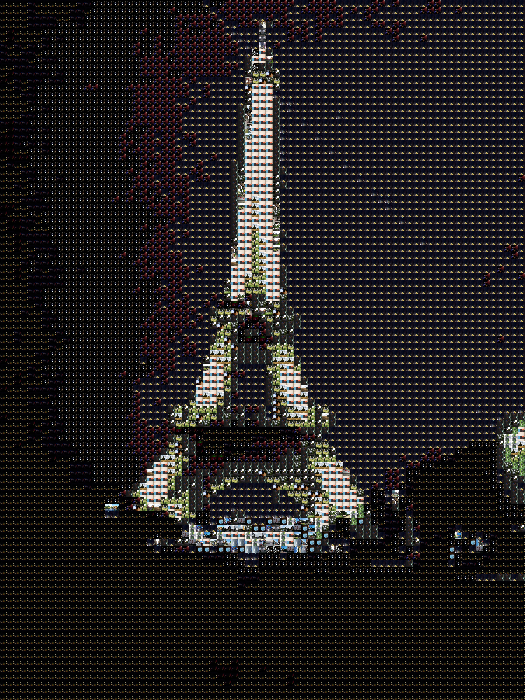
Additional comments
So this was also a small project I did a few years ago (it was written in Java, had a GUI and everything, even a progress bar!) but now I rewrote it in python because yay, python.
The images shown here are just for example and are really bad because I used an album with only 100 photos to get the colors from. For better results use more photos. The photos you use to build the mosaic from don't have to be big so you can resize them to make the first part (calculating all the available colors) faster.
The code here assumes that the image dimensions will be divisible by the number of patches you tell it to use in the configuration, have that in mind.
There are some things that could be done to make the mosaics more interesting, for example:
- Don't calculate the average color of each image as a whole, but split each image into parts, calculate the averages of each part and then choose the best patch to put into the big image based on the part color averages.
- Maybe try having a lot of photos to generate the colors from and try using each photo only once. Could be interesting.
- Make the mosaic infinite! That would be a mosaic consisting of mosaics consisting of mosaics consisting of mosaics and so on and on and on and on etc
That's it! Have fun, bye!